LIBGDX Vector direccion
Introdución
Nota: Esta explicación está relacionada coa sección 'Movendo os gráficos'.
En case todos os xogos imos ter a necesidade de facer que o noso protagonista ou algún inimigo se mova cara a algo.
Por exemplo, imaxinemos que temos un xogo no que disparamos un foguete e queremos que este se dirixa cara un certo punto.
Para conseguir isto imos explicar o que é un vector dirección.
Movendo os gráficos. Vector dirección
Normalmente en todos os xogo ides ter algún personaxe que se mova cara a algún outro personaxe. Por exemplo, cando disparedes queredes que as balas se movan cara o obxectivo.
Para conseguir isto imos facer uso do que se chama Vector Dirección.
Primeiro imos temos que saber o que é un Vector. De forma resumida para nós o Vector vai representar a dirección que ten que seguir un personaxe para chegar a un punto de destino.
Se dito punto de destino non varía no tempo o vector de dirección ten que calcularse ó principio e non variará. Se queremos seguir a un personaxe que se move, cada certo tempo teremos que re-calcular dito vector dirección.
A forma máis sinxela de velo é cun exemplo.
Nota: Os concepto aprendidos serán igualmente aplicables a 3D introducindo a coordenada Z.
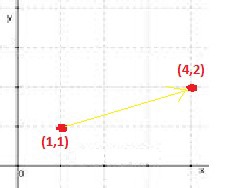
Imaxinemos que estamos na coordenada (1,1) e queremos dirixirnos ata a coordenada (4,2). O que teríamos que facer é calcular cal é o vector de dirección, é dicir, que números (x,y) sumados a (1,1) nos levan ata o (4,2).
O máis lóxico é restar o punto de destino menos o punto de orixe, desta forma:
- Vector Dirección = Punto_Destino – Punto_Orixe = (4,2)-(1,1) = (3,1).
En libgdx o faremos utilizando os métodos sub (para restar dous vectores) e cpy (para facer unha copia do vector) da clase Vector2 (con 3 coordenadas usamos un Vector3 e con dous Vector2):
- Punto Orixe = Posición do personaxe = Vector2 posicion
- Punto Destino = Posición do punto de destino (no exemplo) = Vector2 (4,2)
- direccion = posicion_destino.cpy().sub(posicion_orixe);
Fixarse como usamos unha copia do vector de posición destino xa que o método sub modifica o
vector orixinal.
Se queremos aumentar o rendemento (xa que estamos a facer new´s ó usar a función cpy) teríamos un vector temporal xa creado previamente (no constructor) e copiaríamos o contido chamando ó método set da forma:
- temporal.set(posicion_destino);
- direccion = temporal.sub(posicion_orixe);
Nota: Isto só ten sentido se estamos a chamar ó método cpy de forma continua ou se necesitamos gardar o vector posicion_destino para algo. Se, por exemplo, non modificamos o vector dirección, isto só o temos que facer unha vez no constructor e polo tanto non necesitamos vector temporal para esta operación.
No exemplo anterior teríamos un vector de dirección con valores (3,1).
Agora poderíamos chegar ó punto de destino dun único salto, xa que na primeira iteración sumaríamos o seu valor e xa chegaríamos.
- posicion = posicion + vector_dirección = (1,1) + (3,1) = (4,2).
Isto é debido a que a súa lonxitude é moi grande.
Como o que queremos é que pouco a pouco vaia chegando podemos facer uso do método nor() que normaliza o vector e fai que o seu valor sexa o vector unidade (para nos terá un valor <=1) pero os seus valores farán que ó sumalos á posición se vaia achegando ó punto de destino.
A forma de facer uso del sería a de normalizar o vector dirección antes de sumalo:
- direccion.nor();
Nota: Loxicamente isto só o temos que facer unha vez xa que nor modifica o vector de dirección. Se volvemos aplicar dito método o faríamos sobre o vector xa previamente normalizado. Isto só será necesario facelo cada vez que modifiquemos o vector dirección.
Agora para mover o personaxe ó punto de destino teríamos que facer:
- posicion.add(direccion.cpy().scl(velocidade*delta));
Nota: Igual que no caso anterior podemos usar o mesmo vector temporal para asinarlle antes a dirección e non ter que facer un cpy de cada vez. Normalmente teremos que utilizalo nesta operación.
O método scl multiplica o vector por un escalar (no exemplo o escalar velocidade*delta).
Exemplo de código
Exercicio proposto: Facer que unha bolboreta se mova cara o punto premido na pantalla.
Preparación:
- Copiade a seguinte imaxe ó cartafol assets:
- Crear unha nova clase.
Clase Bolboreta:
import com.badlogic.gdx.math.Vector2;
public class Bolboreta {
public Vector2 direccion,temporal;
public Vector2 tamano,posicion;
public float velocidade,velocidade_max;
public Vector2 puntoDestino;
public Bolboreta(Vector2 posicion, Vector2 tamano, float velocidade_max) {
this.posicion=posicion;
this.tamano = tamano;
this.velocidade_max=velocidade_max;
temporal = new Vector2();
direccion = new Vector2(0,0);
puntoDestino = new Vector2();
}
public void update(float delta){
temporal.set(direccion);
posicion.add(temporal.scl(velocidade_max*delta));
}
}
Nota: Por motivos de tempo non facemos os métodos get e set.
- Liña 24: Utilizamos un vector temporal para gardar a dirección, xa que na seguinte liña facemos unha operación de multiplicación que afectaría o vector.
- Liña 25: Movemos a bolboreta en función do vector dirección.
Clase VectorDireccion:
import com.badlogic.gdx.ApplicationAdapter;
import com.badlogic.gdx.Gdx;
import com.badlogic.gdx.InputProcessor;
import com.badlogic.gdx.graphics.GL20;
import com.badlogic.gdx.graphics.OrthographicCamera;
import com.badlogic.gdx.graphics.Texture;
import com.badlogic.gdx.graphics.g2d.SpriteBatch;
import com.badlogic.gdx.math.Vector2;
import com.badlogic.gdx.math.Vector3;
public class VectorDireccion extends ApplicationAdapter implements InputProcessor{
private SpriteBatch batch;
private Texture img;
private Bolboreta bolboreta;
private OrthographicCamera camara2d;
@Override
public void create () {
batch = new SpriteBatch();
img = new Texture("LIBGDX_GRAFICO_mariposa.png");
bolboreta = new Bolboreta(new Vector2(30,30),new Vector2(50,50),100f);
camara2d = new OrthographicCamera();
camara2d.setToOrtho(false,500f,500f);
camara2d.update();
batch.setProjectionMatrix(camara2d.combined);
Gdx.input.setInputProcessor(this);
}
@Override
public void render() {
Gdx.gl.glClearColor(1, 1, 1, 1);
Gdx.gl.glClear(GL20.GL_COLOR_BUFFER_BIT);
bolboreta.update(Gdx.graphics.getDeltaTime());
batch.begin();
batch.draw(img, bolboreta.posicion.x, bolboreta.posicion.y);
batch.end();
}
@Override
public void dispose() {
img.dispose();
batch.dispose();
Gdx.input.setInputProcessor(null);
}
@Override
public boolean keyDown(int keycode) {
// TODO Auto-generated method stub
return false;
}
@Override
public boolean keyUp(int keycode) {
// TODO Auto-generated method stub
return false;
}
@Override
public boolean keyTyped(char character) {
// TODO Auto-generated method stub
return false;
}
@Override
public boolean touchDown(int screenX, int screenY, int pointer, int button) {
// TODO Auto-generated method stub
Vector3 novopunto = new Vector3(screenX,screenY,0);
camara2d.unproject(novopunto);
bolboreta.puntoDestino.set(new Vector2(novopunto.x,novopunto.y));
Vector2 direccion = bolboreta.puntoDestino.cpy().sub(bolboreta.posicion);
bolboreta.direccion.set(direccion.nor());
return false;
}
@Override
public boolean touchUp(int screenX, int screenY, int pointer, int button) {
// TODO Auto-generated method stub
return false;
}
@Override
public boolean touchDragged(int screenX, int screenY, int pointer) {
// TODO Auto-generated method stub
return false;
}
@Override
public boolean mouseMoved(int screenX, int screenY) {
// TODO Auto-generated method stub
return false;
}
@Override
public boolean scrolled(int amount) {
// TODO Auto-generated method stub
return false;
}
}
- Liña 76-77: Calculamos o punto de destino (onde ten que chegar a bolboreta). Debemos facer un unProyect do mesmo.
- Liña 79: O punto de destino da bolboreta é o que devolve a cámara ortográfica (pero só nas coordenadas x - y).
- Liñas 81-82: Calculamos o vector dirección e o asinamos á bolboreta. Cando chamemos ó método update da bolboreta xa se move en función do novo valor do vector dirección.
Podedes probar agora como a bolboreta se dirixe cara ó punto indicado.
TAREFA OPTATIVA A FACER
TAREFA OPTATIVA A FACER: Utilizando o gráfico anterior ou outro elixido por ti, crea un novo tipo de inimigo que cada certo tempo se dirixa cara á posición do alien.
Posteriormente, cando chegues a sección das colisións deberás xestionar cando o inimigo alcanza ó alien e matalo.
-- Ángel D. Fernández González -- (2014).