LIBGDX Animacions3D
UNIDADE 4: Animacións en 3D
Introdución
Neste apartado imos ver como podemos animar (mover, trasladar e rotar) os obxectos 3D.
Como ven pensades, imos necesitar unha matriz :)
O que imos facer será animar un cubo.
Preparación:
- Copiar a seguinte textura ó cartafol assets do proxecto Android:
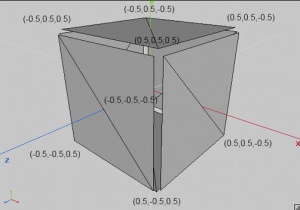
- Imos crear un obxecto Mesh onde imos definir os vértices que conforman os cubos de acordo co seguinte esquema:
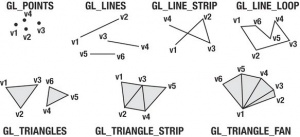
Para facelo imos a utilizar os conceptos aprendidos cos triángulos, pero facendo algunha modificación. Cando fixemos o proxecto dos triángulos definimos dous grupos de vértices, un para cada triángulo. Pero tamén podemos definir os dous triángulos nun mesmo grupo de vértices.
- triangulos = new Mesh(true,6,6,new VertexAttribute(Usage.Position,3,"a_position"),new VertexAttribute(Usage.ColorPacked,4,"a_color"));
- triangulos.setVertices(new float[] {-0.5f,-0.5f,-3f,1f,0,0,1f, 0.5f,-0.5f,-3f,1f,0,0,1f, 0f,0.5f,-3f,1f,0,0,1f, 0f,-0.5f,-5f,1f,0,0,1f, 1f,-0.5f,-5f,1f,0,0,1f, 0.5f,0.5f,-5f,1f,0,0,1f});
- triangulos.setIndices(new short[]{0,1,2,3,4,5});
- .....
- triangulos.render(GL10.GL_TRIANGLES,0,3);
- triangulos.render(GL10.GL_TRIANGLES,3,3);
Está marcado en negrilla os cambios. Agora os vértices están xuntos. Cando debuxamos (render) informamos que imos debuxar un triángulo que ten a información dos vértices no array de vértices. Un dos triángulos empeza na posición 0 do array e ten tres vértices, mentres que o triángulo2 empeza na posición 3 e ten tres vértices.
A orde de debuxo dos vértices ven indicado polo array de índices (triángulo1 => 0,1,2 ; triángulo2 => 3,4,5).
Nota: Poderíamos aproveitar os triángulos que comparten lados e aforrarnos puntos no array de
vértices.
Volvendo ó Cubo, vemos que cada lado do cubo vai necesitar 4 vértices, por 6 caras = 24 vértices. Por outra banda cada triángulo necesita 3 índices. Se cada cara ten dous triángulos isto da:
- 3 índices por triángulo x 2 triángulos por cara x 6 caras = 36 índices.
Crear unha clase de nome Shapes. Dita clase o que vai definir será un Cubo cos seus vértices e índices así como as coordenadas da textura.
Código da clase Shapes
Obxectivo: Xera un obxecto Mesh coa forma dun cubo en 3D.
import com.badlogic.gdx.graphics.Mesh;
import com.badlogic.gdx.graphics.VertexAttribute;
public class Shapes {
public static Mesh genCube() {
Mesh mesh = new Mesh(true, 24, 36, VertexAttribute.Position(),VertexAttribute.TexCoords(0));
float[] vertices = { -0.5f, -0.5f, 0.5f, 0, 1, 0.5f, -0.5f, 0.5f, 1, 1,
0.5f, 0.5f, 0.5f, 1, 0, -0.5f, 0.5f, 0.5f, 0, 0, 0.5f, -0.5f,
0.5f, 0, 1, 0.5f, -0.5f, -0.5f, 1, 1, 0.5f, 0.5f, -0.5f, 1, 0,
0.5f, 0.5f, 0.5f, 0, 0, 0.5f, -0.5f, -0.5f, 0, 1, -0.5f, -0.5f,
-0.5f, 1, 1, -0.5f, 0.5f, -0.5f, 1, 0, 0.5f, 0.5f, -0.5f, 0, 0,
-0.5f, -0.5f, -0.5f, 0, 1, -0.5f, -0.5f, 0.5f, 1, 1, -0.5f,
0.5f, 0.5f, 1, 0, -0.5f, 0.5f, -0.5f, 0, 0, -0.5f, 0.5f, 0.5f,
0, 1, 0.5f, 0.5f, 0.5f, 1, 1, 0.5f, 0.5f, -0.5f, 1, 0, -0.5f,
0.5f, -0.5f, 0, 0, -0.5f, -0.5f, 0.5f, 0, 1, 0.5f, -0.5f, 0.5f,
1, 1, 0.5f, -0.5f, -0.5f, 1, 0, -0.5f, -0.5f, -0.5f, 0, 0 };
short[] indices = { 0, 1, 3, 1, 2, 3, 4, 5, 7, 5, 6, 7, 8, 9, 11, 9,
10, 11, 12, 13, 15, 13, 14, 15, 16, 17, 19, 17, 18, 19, 20, 21,
23, 21, 22, 23, };
mesh.setVertices(vertices);
mesh.setIndices(indices);
return mesh;
}
}
Como vemos non mandamos información de cor, só posición e textura polo que temos que modificar os arquivos de vertex.vert e fragment.frag.
- Arquivo vertex.vert:
attribute vec3 a_position;
attribute vec2 a_texCoord0;
varying vec2 v_textCoord;
uniform mat4 u_worldView;
void main()
{
gl_Position = u_worldView *vec4(a_position,1);
v_textCoord = a_texCoord0;
}
- Arquivo fragment.frag:
#ifdef GL_ES
precision mediump float;
#endif
varying vec2 v_textCoord;
uniform sampler2D u_texture;
void main()
{
vec4 texColor = texture2D(u_texture, v_textCoord);
gl_FragColor = texColor;
}
- Crear unha clase de nome UD4_5_Animacion3D, que derive da clase Game e sexa chamada pola clase principal das diferentes versións (desktop, android,...).
Código da clase UD4_5_Animacion3D
Obxectivo: Visualiza un cubo en 3D cunha cámara en perspectiva.
import com.badlogic.gdx.Game;
import com.badlogic.gdx.Gdx;
import com.badlogic.gdx.files.FileHandle;
import com.badlogic.gdx.graphics.GL20;
import com.badlogic.gdx.graphics.Mesh;
import com.badlogic.gdx.graphics.PerspectiveCamera;
import com.badlogic.gdx.graphics.Texture;
import com.badlogic.gdx.graphics.glutils.ShaderProgram;
/**
* Funcionamento do ShaderProgram
* @author ANGEL
*/
public class UD4_5_Animacion3D extends Game {
private Mesh cubo;
private ShaderProgram shaderProgram;
private Texture textura;
private PerspectiveCamera camara3d;
@Override
public void create() {
// TODO Auto-generated method stub
shaderProgram = new ShaderProgram(Gdx.files.internal("vertex.vert"), Gdx.files.internal("fragment.frag"));
if (shaderProgram.isCompiled() == false) {
Gdx.app.log("ShaderError", shaderProgram.getLog());
System.exit(0);
}
cubo = Shapes.genCube();
FileHandle imageFileHandle = Gdx.files.internal("crate.png");
textura = new Texture(imageFileHandle);
camara3d = new PerspectiveCamera();
}
@Override
public void render() {
Gdx.gl20.glClearColor(0f, 0f, 0f, 1f);
Gdx.gl20.glClear(GL20.GL_COLOR_BUFFER_BIT|GL20.GL_DEPTH_BUFFER_BIT);
Gdx.gl20.glEnable(GL20.GL_DEPTH_TEST);
shaderProgram.begin();
shaderProgram.setUniformMatrix("u_worldView", camara3d.combined);
textura.bind(0);
shaderProgram.setUniformi("u_texture", 0);
cubo.render(shaderProgram, GL20.GL_TRIANGLES);
shaderProgram.end();
Gdx.gl20.glDisable(GL20.GL_DEPTH_TEST);
}
@Override
public void resize (int width,int height){
// Definimos os parámetros da cámara
float aspectRatio = (float) width / (float) height;
camara3d.viewportWidth=aspectRatio*1f;
camara3d.viewportHeight=1f;
camara3d.far=1000f;
camara3d.near=0.1f;
camara3d.lookAt(0,0,0);
camara3d.position.set(0f,0f,5f);
camara3d.update();
}
@Override
public void dispose(){
shaderProgram.dispose();
cubo.dispose();
}
}
Se probades a executar o código aparecerá un cubo na pantalla.
Nota: Loxicamente os modelos 3D non os temos que definir desta forma, se non que usaremos programas de deseño en 3D ou modelos xa feitos.
Animando o cubo: translación, rotación e escalado
Clase utilizada: Matrix4.
Información na wiki: https://github.com/libgdx/libgdx/wiki/Vectors,-matrices,-quaternions
En OPEN GL imos poder facer tres tipos de operacións:
- TRASLACIÓN: Lembrar que por defecto todos os obxectos se debuxan nas coordenadas (0,0,0). No noso mundo os obxectos (figuras Mesh) estarán nunha posición no espazo 3D. Será necesario trasladalos dende a posición (0,0,0) á posición no noso mundo.
- ROTACIÓN: Podemos rotar a figura Mesh en calquera dos eixes (x,y,z). Lembrar que para saber como se rota a figura en cada un deles temos que imaxinar que a nosa cabeza está atravesado por unha lanza en cada un dos eixes. Así:
- Eixe X: Moveríamos arriba-abaixo.
- Eixe Y: Moveríamos esquerda-dereita.
- Eixe Z; Moveríamos de lado, levando a cabeza ós ombreiros.
- ESCALADO: O da escala o entenderedes mellor cando vexades o vídeo de como facer unha figura xeométrica 3D nun programa de deseño. Nestes programas a visualización 3D está dividida en cadrados. Cada cadrado ven ser unha unidade, de tal forma que se achegamos a cámara ata o obxecto, por defecto , o ancho e alto da cámara será dunha unidade. O que nos interesa é facer os obxectos de forma proporcional uns con outros. Así, se teño un modelo dun coche e está ocupando 4 unidades, se agora engado un deseño dun barco, non pode ser que o barco ocupe 4 unidades. Proporcionalmente ten que haber unha relación entre un modelo e outro.
Como ven vos estaredes imaxinando imos necesitar gardar unha matriz, unha matriz de modelado. Esta matriz é un vector 4x4.
Exemplo de definición de matriz:
public Matrix4 matriz;
A matriz que aparece na imaxe se denomina matriz de identidade e ven a ser o número 1 na multiplicación, é dicir, que non fai nada.
Para cargar a matriz de identidade temos que chamar ó método idt():
public Matrix4 matriz;
..........
matriz.idt();
Agora será necesario aplicar os 3 tipos de operacións:
- Traslación:
- Método translate:
- Exemplo: matriz.translate(posicion);
- Sendo 'posicion' un Vector3 que indica cara onde se ten que trasladar. Este método está sobrecargado e temos varias opcións.
- É importante comprender que sempre debemos de partir da matriz identidade e aplicar a nova posición que queremos chegar. Non o podemos facer a partires da última posición gardada.
Exemplo de código:
public Matrix4 matriz;
..........
matriz.idt();
matriz.translate(10,1,0);
- Rotación:
- Este método está sobrecargado e temos varias posibilidades.
Un exemplo:
public Matrix4 matriz;
..........
matriz.idt();
matriz.translate(10,1,0);
matriz.rotate(1,0,0,90);
Neste caso estaremos rotando no eixe X a figura 90º. Neste caso o método rotate leva catro parámetros:
- param1: Indica se o eixe X debe rotarse. Se ten valor 1 o rota e se ten 0 non fai nada nese eixe.
- param2: Indica se o eixe Y debe rotarse. Se ten valor 1 o rota e se ten 0 non fai nada nese eixe.
- param3: Indica se o eixe Z debe rotarse. Se ten valor 1 o rota e se ten 0 non fai nada nese eixe.
- param4: Indica o número de grados da rotación.
Aviso: É importante primeiro facer a traslación e despois a rotación, xa que se o facemos ó revés, o punto está rotado cando aplicamos a traslación e por tanto se moverá a outro lugar diferente o que queremos. Se o fixeramos cunha esfera, teríamos o efecto dun movemento de traslación arredor do sol.
- Escala:
Podemos modificar a escala en cada un dos eixes (X-Y-Z).
Por exemplo:
public Matrix4 matriz;
..........
matriz.idt();
matriz.translate(10,1,0);
matriz.rotate(1,0,0,90);
matriz.scale(2,1,1);
Neste exemplo indicamos que o tamaño X da figura debe ser o dobre que o tamaño Y e Z.
Moi ben, chegou a hora de mover ese cubo :).
Preparación: Sen programar totalmente seguindo o MVC imos definir o noso mundo cun array de cubos. A clase Cubo terá a información necesaria, que será parecida a que tiñamos cando fixemos o xogo en 2D, pero tendo en conta as particularidades do 3D.
Código da clase Cubo
Obxectivo: Definimos a clase Cubo para engadir cubos ó noso mundo.
import com.badlogic.gdx.math.Matrix4;
import com.badlogic.gdx.math.Vector3;
public class Cubo {
public Matrix4 matriz;
public Vector3 posicion;
public float escala;
public Vector3 velocidade;
private float rotar;
private Vector3 temp;
public Cubo(Vector3 pos, float escala,Vector3 velocidade){
matriz = new Matrix4();
posicion = pos;
this.escala=escala;
this.velocidade = velocidade;
temp = new Vector3();
}
public void update(float delta){
temp.set(velocidade);
posicion.add(temp.scl(delta));
matriz.idt();
matriz.translate(posicion);
}
}
Comentemos o código:
- Liñas 6-11: O que necesitamos gardar da figura.
- Liña 6: A matriz de modelado que vai gardar os datos necesarios a aplicar en cada punto do Mesh.
- Liña 7: Como vemos temos unha posición (Vector3). Aplicaremos ó método translate sobre a matriz.
- Liña 8: A escala (que vai ser aplicada ós tres eixes) e que tamén pode non ser necesaria, dependendo do xogo.
- Liña 9: A velocidade. Tamén pode non ser necesaria (se non se move). Neste caso poderíamos ter diferentes velocidades en cada un dos eixes. Se a velocidade é a mesma en calquera dos eixes no que se mova podería ser un float en vez dun Vector3.
- Liña 10: O ángulo de rotación, pero se no noso xogo non o necesitamos podemos eliminar esta propiedade.
- Liña 11: Vector temporal para non ten que estar creando novos no método update. Lembrar que os métodos cpy, scl,...aplicados a un vector3 modifican o vector orixinal.
- Liñas 14-22: Gardamos nas propiedades os valores enviados no constructor.
- Liña 26: Modificamos o vector posición en función de delta igual que fixemos no xogo 2D.
- Liñas 28-29: Modificamos a matriz de modelado cos datos da nova posición. Fixarse como temos que partir da matriz identidade (liña 28).
Máis adiante faremos a rotación e escalado. Polo de agora o deixamos así...
Agora chega o momento de definir o mundo:
Código da clase Mundo
Obxectivo: Engadir dous cubos ó mundo.
import java.util.ArrayList;
import com.badlogic.gdx.math.Vector3;
public class Mundo {
public ArrayList<Cubo>cubos;
public Mundo(){
cubos = new ArrayList<Cubo>();
cubos.add(new Cubo(new Vector3(0,0,-3f),1f,new Vector3(1,0,0)));
cubos.add(new Cubo(new Vector3(4f,0,-3f),5f,new Vector3(-1,0,0)));
}
}
Esta clase non ten nada que comentar. Creamos dous cubos.
Agora chega o momento de pasarlle esta matriz ó Shader Program para que teña en conta onde están situados os puntos. Para iso temos que multiplicar a matriz combinada da cámara coa matriz de modelado do obxecto, pero tendo coidado de ter gardada a matriz combinada xa que a operación de multiplicación modifica a matriz.
Código da clase UD4_5_Animacion3D
Obxectivo: Movemos os cubos.
@Override
public void render() {
Gdx.gl20.glClearColor(0f, 0f, 0f, 1f);
Gdx.gl20.glClear(GL20.GL_COLOR_BUFFER_BIT|GL20.GL_DEPTH_BUFFER_BIT);
Gdx.gl20.glEnable(GL20.GL_DEPTH_TEST);
shaderProgram.begin();
textura.bind(0);
shaderProgram.setUniformi("u_texture", 0);
for (Cubo cub : mundo.cubos){
cub.update(Gdx.graphics.getDeltaTime());
shaderProgram.setUniformMatrix("u_worldView", camara3d.combined.cpy().mul(cub.matriz));
cubo.render(shaderProgram, GL20.GL_TRIANGLES);
if (Math.abs(cub.posicion.x)>=10){
cub.velocidade.x *=-1;
}
}
shaderProgram.end();
Gdx.gl20.glDisable(GL20.GL_DEPTH_TEST);
}
Liña 17: Por cada cubo do mundo (estamos a percorrer o array) multiplicamos unha copia da matriz combinada da cámara, polo matriz de modelado do obxecto. Chamamos ó método cpy() para facer unha copia. O ideal é ter unha matriz temporal xa instanciada no constructor e asinarlle o valor da matriz combinada antes de multiplicar.
Liña 20-22: Código posto para que os cubos cambien de dirección.
Imos modificar ó método update da clase Cubo para que rote e escale os cubos de acordo ós datos enviados no constructor.
public void update(float delta){
temp.set(velocidade);
posicion.add(temp.scl(delta));
rotar+=60f*delta;
matriz.idt();
matriz.translate(posicion);
matriz.scl(escala);
matriz.rotate(1, 1, 1, rotar);
}
- Liña 6: Gardamos o ángulo de rotación.
- Liña 10: Escalamos a matriz en todos os eixes.
- Liñá 11: Rotamos a matriz en todos os eixes.
Dará como resultado isto:
Como vemos un dos cubos é moi grande pola escala que enviamos no constructor.
NOTA: Lembrar que cando fagamos unha rotación, primeiro debemos de aplicar a escala á matriz.
-- Ángel D. Fernández González -- (2014).