LIBGDX Movendo os graficos avanzado

Movendo os gráficos. Vector dirección

Normalmente en todos os xogo ides ter algún personaxe que se mova cara a algún outro personaxe. Por exemplo, cando disparedes queredes que as balas se movan cara o obxectivo.

No noso caso imos facer que aleatoriamente as bolboretas ó aparecer vaian cara á bolboreta Candela, para obrigala a movela.

Para conseguir isto imos facer uso do que se chama Vector Dirección.

Primeiro imos temos que saber o que é un Vector. De forma resumida para nós o Vector vai representar a dirección que ten que seguir un personaxe para chegar a un punto de destino.

Se dito punto de destino non varía no tempo o vector de dirección ten que calcularse ó principio e non variará. Se queremos seguir a un personaxe que se move, cada certo tempo teremos que re-calcular dito vector dirección.

A forma máis sinxela de velo é cun exemplo.

Nota: Os concepto aprendidos serán igualmente aplicables a 3D introducindo a coordenada Z.

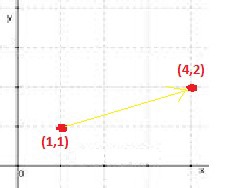
Imaxinemos que estamos na coordenada (1,1) e queremos dirixirnos ata a coordenada (4,2). O que teríamos que facer é calcular cal é o vector de dirección, é dicir, que números (x,y) sumados a (1,1) nos levan ata o (4,2).

O máis lóxico é restar o punto de destino menos o punto de orixe, desta forma:

Vector Dirección = Punto_Destino – Punto_Orixe = (4,2)-(1,1) = (3,1).

En libgdx o faremos utilizando os métodos sub (para restar dous vectores) e cpy (para facer unha copia do vector) da clase Vector2 (con 3 coordenadas usamos un Vector3 e con dous Vector2):

Punto Orixe = Posición do personaxe = Vector2 posicion

Punto Destino = Posición do punto de destino (no exemplo) = Vector2 (4,2)

direccion = posicion_destino.cpy().sub(posicion_orixe);

Fixarse como usamos unha copia do vector de posición destino xa que o método sub modifica o vector orixinal.

Se queremos aumentar o rendemento (xa que estamos a facer new´s ó usar a función cpy) teríamos un vector temporal xa creado previamente (no constructor) e copiaríamos o contido chamando ó método set da forma:

temporal.set(posicion_destino);

direccion = temporal.sub(posicion_orixe);

Nota: Isto só ten sentido se estamos a chamar ó método cpy de forma continua ou se necesitamos gardar o vector posicion_destino para algo. Se, por exemplo, non modificamos o vector dirección, isto só o temos que facer unha vez no constructor e polo tanto non necesitamos vector temporal para esta operación.

No exemplo anterior teríamos un vector de dirección con valores (3,1). Agora poderíamos chegar ó punto de destino dun único salto, xa que na primeira iteración sumaríamos o seu valor e xa chegaríamos.

posicion = posicion + vector_dirección = (1,1) + (3,1) = (4,2).

Isto é debido a que a súa lonxitude é moi grande. Como o que queremos é que pouco a pouco vaia chegando podemos facer uso do método nor() que normaliza o vector e fai que o seu valor sexa o vector unidade (para nos terá un valor <=1) pero os seus valores farán que ó sumalos á posición se vaia achegando ó punto de destino.

A forma de facer uso del sería a de normalizar o vector dirección antes de sumalo:

direccion.nor();

Nota: Loxicamente isto só o temos que facer unha vez xa que nor modifica o vector de dirección. Se volvemos aplicar dito método o faríamos sobre o vector xa previamente normalizado. Isto só será necesario facelo cada vez que modifiquemos o vector dirección.

Agora para mover o personaxe ó punto de destino teríamos que facer:

posicion.add(direccion.cpy().scl(velocidade*delta));

Nota: Igual que no caso anterior podemos usar o mesmo vector temporal para asinarlle antes a dirección e non ter que facer un cpy de cada vez. Normalmente teremos que utilizalo nesta operación.

O método scl multiplica o vector por un escalar (no exemplo o escalar velocidade*delta).

Imos poñer en práctica os conceptos aprendidos.

Exercicio proposto: Facer que as bolboretas se dirixan ó punto 500,300 do noso mundo (esquina superior dereita).

Preparación: Agora ides facer unha copia da clase UD2_4_RendererXogo, xa que imos modificala para amosarvos como se poden mover os gráficos cara a un punto. Premede co rato sobre a clase, botón dereito e escollede a opción Copy. Despois repetides a operación pero escolledes a opción Paste. Vos preguntará un nome para a clase. Indicade UD2_5_RendererXogo. Modificade a clase PantallaXogo para que chame á nova clase.

Solución:

• Primeiro definimos o vector dirección na clase bolboreta e o instanciamos no constructor. Tamén definimos e instaciamos un vector temporal polo visto anteriormente.

O vector temporal o usaremos despois cando vexamos o modelo-vista-controlador.

• Creamos un constructor novo para darlle o punto final ó que se ten que dirixir a bolboreta. Tamén creamos un método setDireccion que terá como parámetro un novo punto final para cambiar a dirección en caso necesario e un método getDireccion que devolva dito vector.

Clase Bolboreta:

public class Bolboreta extends Personaxe {

	public static enum TIPOS_BOLBORETAS {CANDELA, INIMIGA1, INIMIGA2, INIMIGA3}
	
	private TIPOS_BOLBORETAS tipo_bolboreta;
	
	private Vector2 direccion,temporal;
	
	public Bolboreta(Vector2 posicion, Vector2 tamano, float velocidade_max,TIPOS_BOLBORETAS tipo_bolboreta) {

		super(posicion, tamano, velocidade_max);
		this.tipo_bolboreta=tipo_bolboreta;

		setVelocidade(velocidade_max);	// Facemos que por defecto todas as bolboretas se movan á velocidade indicada.
	}

	public Bolboreta(Vector2 posicion, Vector2 tamano, float velocidade_max,TIPOS_BOLBORETAS tipo_bolboreta,Vector2 posfinal) {

		this(posicion, tamano, velocidade_max,tipo_bolboreta);
		direccion = posfinal.sub(posicion).nor();
		temporal = new Vector2();
	}
         /**
	 * Modifica o vector dirección
	 * @param puntofinal: novo punto final
	 */
	public void setDireccion(Vector2 puntofinal){
		direccion.set(puntofinal.sub(posicion).nor());
	}
	public Vector2 getDireccion(){
		return direccion;
	}

        ...................

• Modificamos a clase Mundo para crear as bolboretas dándolle o punto final onde ten que dirixirse (500,300)

Clase Mundo:

    public Mundo(){
    	candela = new Candela(new Vector2(30,30), new Vector2(15,15),100,Bolboreta.TIPOS_BOLBORETAS.CANDELA);
    	bolboretas = new Array<Bolboreta>();
    	
    	bolboretas.add(new Bolboreta(new Vector2(40,250),new Vector2(10,10),80,Bolboreta.TIPOS_BOLBORETAS.INIMIGA1, new Vector2(500,300)));
    	bolboretas.add(new Bolboreta(new Vector2(20,50),new Vector2(10,10),70,Bolboreta.TIPOS_BOLBORETAS.INIMIGA2,new Vector2(500,300)));
    	
    }

• Despois modificamos o método debuxarBolboretas da clase UD_2_5_RendererXogo para que a bolboreta se mova segundo o indicado polo vector dirección.

Clase UD_2_5_RendererXogo:

	private void debuxarBolboretas(){
		Texture tempTextura=null;
		
		for (Bolboreta bolboreta : meumundo.getBolboretas()){
			if (bolboreta.getTipo_bolboreta()==Bolboreta.TIPOS_BOLBORETAS.INIMIGA1){
				tempTextura = AssetsXogo.mariposa_e1;
			}
			else if (bolboreta.getTipo_bolboreta()==Bolboreta.TIPOS_BOLBORETAS.INIMIGA2){
				tempTextura = AssetsXogo.mariposa_e2;
			}
			else tempTextura = AssetsXogo.mariposa_e3;
			
 			  bolboreta.getPosicion().add(bolboreta.getDireccion().cpy().scl(66*Gdx.graphics.getDeltaTime()));
			spritebatch.draw(tempTextura, 
					bolboreta.getPosicion().x,bolboreta.getPosicion().y,
					bolboreta.getTamano().x, bolboreta.getTamano().x);
			
		}
	}

Podedes probar agora como as bolboretas se dirixen ó punto indicado.

Cambiade a clase PantallaXogo para que volva a chamar á clase RendererXogo.

-- Ángel D. Fernández González -- (2014).